Magnetvälja kehtiv totaalne seadus: valemid ja määratlus

Paljudele tuttav teema "Elektrotehnika" sisaldab oma programmis mitmeid põhiseadusi, mis määravad kindlaks magnetvälja füüsilise interaktsiooni põhimõtted. Nad laiendavad oma tegevust elektriseadmete erinevatele elementidele, samuti nende koostisosadele ja keskkonnale. Neis toimuvate protsesside füüsika puudutab selliseid põhikontseptsioone nagu elektrivood ja väljad. Täisvoolu seadus kehtestab seose elektrilaengute liikumise ja selle tekitatud magnetvälja (täpsemalt selle intensiivsuse) vahel. Kaasaegne teadus väidab, et selle rakendus hõlmab peaaegu kõiki keskkondi.

Seaduse olemus

Kaalutud seadus, mida kohaldatakse magnetvooluahelates, määrab selle komponentide vahel järgmise kvantitatiivse seose. Magnetvälja vektori ringlus suletud ahelas on võrdeline seda läbivate voolude summaga. Täisvoolu seaduse füüsilise tähenduse mõistmiseks peate tutvuma selle kirjeldatud protsesside graafilise esitusega.

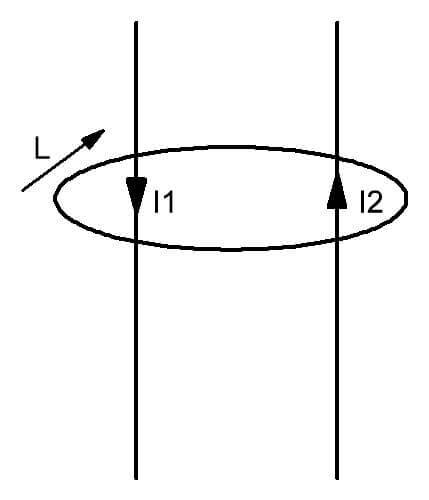
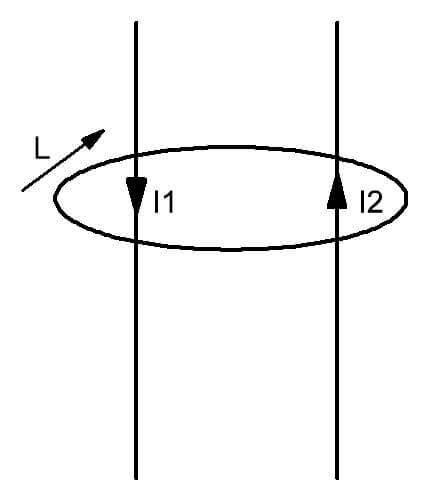
Jooniselt on näha, et kahe juhi ümber, mille voolud I1 ja I2 voolavad, moodustub väli, mida piirab kontuur L. Seda tutvustatakse vaimselt ettekujutatud suletud kujundina, mille tasapinda läbivad liikuva laenguga juhid. Lihtsate sõnadega saab seda seadust väljendada järgmiselt. Mitme elektrivoolu juuresolekul läbi kontuuri L kaetud kujuteldava pinna moodustub selle sees kindla intensiivsuse jaotusega magnetväli.

Vektori positiivse liikumissuuna jaoks valitakse vastavalt magnetahela kontuuri seadusele päripäeva liikumine. See on ka visualiseeritud.

Selline hoovuste loodud pöörisvälja määratlus eeldab, et iga hoovuse suund võib olla meelevaldne.

Viitamiseks! Sissejuhatav väljastruktuur ja seda kirjeldav aparaat tuleks eristada elektrostaatilise vektori "E" ringlusest, mis on kontuuri mööda minnes alati null. Seetõttu viitab selline väli potentsiaalsetele struktuuridele. Magnetvälja vektori "B" ringlus ei ole kunagi null. Sellepärast nimetatakse seda "keeriseks".

Põhimõisted

Vastavalt vaadeldavale seadusele kasutatakse magnetväljade arvutamiseks järgmist lihtsustatud meetodit. Koguvoolu esitatakse mitme komponendi summana, mis voolavad läbi suletud ahelaga kaetud pinna. Teoreetilisi arvutusi saab esitada järgmiselt:

1. Kontuuri rating I läbiv kogu elektrivoo on I1 ja I2 vektorite summa.
2. Vaadeldavas näites kasutatakse selle määramiseks valemit:
   ΣI = I1- I2 (miinus enne teist terminit tähendab, et voolude suunad on vastupidised).
3. Need omakorda määratakse kindlaks elektrotehnikas tuntud seaduse (reegli) järgi kardaan.

Magnetvälja tugevus piki kontuuri arvutatakse spetsiaalsete tehnikate abil saadud arvutuste põhjal. Selle leidmiseks peate selle parameetri integreerima L -i, kasutades Maxwelli võrrandit, mis on esitatud ühes vormis.Seda saab rakendada ka diferentseeritud kujul, kuid see muudab arvutused mõnevõrra keerulisemaks.

Integreeritud lihtsustatud lähenemisviis

Kui me kasutame diferentseeritud esitusviisi, on praegust kogu seadust lihtsustatud kujul väga raske väljendada (sel juhul tuleb sellesse lisada täiendavaid komponente). Lisame sellele, et kontuuri piires liikuvate voolude tekitatud magnetkeerisväli, määratakse sel juhul, võttes arvesse nihkevoolu, mis sõltub elektrienergia muutumise kiirusest induktsioon.

Seetõttu on praktikas SOE -s kõige populaarsem koguvoolude valemite esitamine vooluahela mikroskoopiliselt väikeste sektsioonide summeerimise kujul, millesse on loodud keeriseväljad. See lähenemisviis hõlmab Maxwelli võrrandi rakendamist integraalsel kujul. Selle rakendamisel jagatakse kontuur väikesteks segmentideks, mida esimesel lähendamisel peetakse sirgjoonelisteks (seaduse kohaselt eeldatakse, et magnetväli on ühtlane). See kogus, mis on tähistatud kui Um vaakumis toimiva magnetvälja ühe eraldiseisva lõigu ΔL jaoks, määratakse järgmiselt:

Um = HL * ΔL

Kogu pinge piki kogu kontuuri L, mis on lühidalt esitatud lahutamatul kujul, leitakse järgmise valemi abil:

UL = Σ HL * ΔL.

Kogu kehtiv seadus vaakumi kohta

Lõplikul kujul, mis on koostatud vastavalt kõigile integratsioonireeglitele, näeb kogu kehtiv seadus välja selline. Vektori "B" ringlust suletud ahelas võib kujutada magnetkonstandi korrutisena m voolude summa kohta:

B integraal üle dL = Bl integraal üle dL = m. Sisse

kus n on mitmesuunaliste vooludega juhtide koguarv, mis on kaetud suvalise kujuga kujuteldava ahelaga L.

Iga voolu loetakse selles valemis nii mitu korda, kui see on selle vooluahelaga täielikult kaetud.

Kogu praeguse seaduse arvutuste lõplikku vormi mõjutab suuresti keskkond, milles indutseeritud elektromagnetiline jõud (väli) toimib.

Keskkonna mõju

Kaalutud suhted vooluseadustele ja väljadele, mis toimivad mitte vaakumis, vaid magnetkeskkonnas, omandavad veidi teistsuguse vormi. Sel juhul tutvustatakse lisaks peamistele voolukomponentidele näiteks magnetis või mis tahes sellega sarnases materjalis tekkivate mikroskoopiliste voolude kontseptsiooni.

Vajalik suhe tuletatakse täielikult magnetilise induktsiooni B vektorringluse teoreemist. Lihtsamalt öeldes väljendatakse seda järgmisel kujul. Vektori B koguväärtus piki valitud kontuuri integreerimisel on võrdne sellega hõlmatud makrovoolude summaga, mis on korrutatud magnetkonstandi koefitsiendiga.

Selle tulemusel määratakse aine valem "B" järgmiselt:

B integraal üle dL = Bl integraal üle dL = m(Mina+Mina1)

kus: dL on vooluahela diskreetne element, mis on suunatud mööda selle ümbersõitu, Bl on komponent puutuja suunas suvalises punktis, bI ja I1 on juhtivusvool ja mikroskoopiline (molekulaarne) vool.

Kui väli toimib keskkonnas, mis koosneb suvalistest materjalidest, tuleb arvestada nendele struktuuridele iseloomulikke mikroskoopilisi voolusid.

Need arvutused kehtivad ka solenoidis või mis tahes muus piiratud magnetilise läbilaskvusega keskkonnas loodud välja puhul.

Viitamiseks

Kõige täielikumas ja põhjalikumas CGS mõõtmissüsteemis on magnetvälja tugevus esindatud oerstedides (E). Teises kehtivas süsteemis (SI) väljendatakse seda amprites meetri kohta (A / meeter). Tänapäeval asendatakse oersted järk -järgult mugavama ühikuga - amprit meetri kohta. Mõõtmiste või arvutuste tulemuste teisendamisel SI -st CGS -i kasutatakse järgmist suhet:

1 E = 1000 / (4π) A / m 9. 79,5775 amprit / meeter.

Ülevaate viimases osas märgime, et olenemata sellest, millist koguvoolude seaduse sõnastust kasutatakse, jääb selle olemus muutumatuks. Tema enda sõnul võib seda kujutada järgmiselt: see väljendab suhet antud vooluringi läbivate voolude ja aines tekkivate magnetväljade vahel.

Lõpuks soovitame vaadata kasulikku videot artikli teemal:

Seotud materjalid:

• Mis on elektriväli
• Juhi takistuse sõltuvus temperatuurist
• Nikola Tesla suurimad avastused