The familiar to many subject called "Electrical Engineering" contains in its program a number of fundamental laws that determine the principles of physical interaction for a magnetic field. They extend their action to various elements of electrical devices, as well as to their constituent structures and environments. The physics of the processes occurring in them concerns such basic concepts as flows of electricity and fields. The law of total current establishes the relationship between the movement of electric charges and the magnetic field created by it (more precisely, its intensity). Modern science claims that its application extends to almost all environments.
Content:
- The essence of the law
- Basic concepts
- Simplified Integral Approach
- Total current law for vacuum
- Influence of the environment
- For reference
The essence of the law
The considered law, applicable in magnetic circuits, determines the following quantitative relationship between its constituents. The circulation of the magnetic field vector in a closed loop is proportional to the sum of the currents flowing through it. To understand the physical meaning of the law of total current, you will need to familiarize yourself with the graphical representation of the processes described by it.
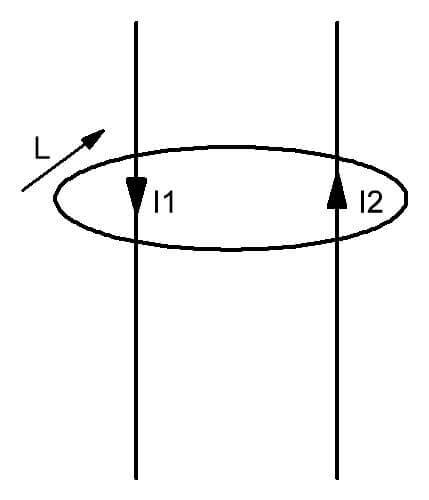
It can be seen from the figure that around two conductors with currents I1 and I2 flowing through them, a field is formed, limited by the circuit L. It is introduced as a mentally imagined closed figure, the plane of which is penetrated by conductors with moving charges. In simple words, this law can be expressed as follows. In the presence of several streams of electricity through the imaginary surface covered by the contour L, a magnetic field with a given distribution of intensity is formed within it.
For the positive direction of movement of the vector, in accordance with the law for the contour of the magnetic circuit, the clockwise movement is selected. It is also visualized.
Such a definition of the eddy field created by the currents assumes that the direction of each of the currents can be arbitrary.
For reference! The introduced field structure and the apparatus describing it should be distinguished from the circulation of the electrostatic vector "E", which is always zero when bypassing the contour. As a consequence, such a field refers to potential structures. The circulation of the vector "B" of the magnetic field is never zero. That is why it is called "vortex".
Basic concepts
In accordance with the law under consideration, the following simplified approach is used to calculate magnetic fields. The total current is represented as the sum of several components flowing through the surface covered by a closed loop L. Theoretical calculations can be presented as follows:
- The total electric flux penetrating the contours Σ I is the vector sum of I1 and I2.
- In the example under consideration, the formula is used to determine it:
ΣI = I1- I2 (minus before the second term means that the directions of the currents are opposite). - They, in turn, are determined according to the well-known law (rule) in electrical engineering gimbal.
The magnetic field strength along the contour is calculated on the basis of the calculations obtained using special techniques. To find it, you will have to integrate this parameter over L using Maxwell's equation, presented in one of the forms.It can also be applied in differential form, but this will complicate calculations somewhat.
Simplified Integral Approach
If we use the differential representation, it will be very difficult to express the total current law in a simplified form (in this case, additional components have to be introduced into it). We add to this that the magnetic vortex field created by currents moving within the contour, is determined in this case taking into account the displacement current, which depends on the rate of change in the electrical induction.
Therefore, in practice, the most popular in SOE is the representation of formulas for total currents in the form of summing microscopically small sections of a circuit with vortex fields created in them. This approach involves the application of the Maxwell equation in integral form. When it is implemented, the contour is divided into small segments, which in the first approximation are considered rectilinear (according to the law, it is assumed that the magnetic field is uniform). This quantity, denoted as Um for one discrete section of length ΔL of the magnetic field acting in vacuum, is determined as follows:
Um = HL * ΔL
The total tension along the complete contour L, presented briefly in integral form, is found by the following formula:
UL = Σ HL * ΔL.
Total current law for vacuum
In its final form, drawn up according to all the rules of integration, the total current law looks like this. Circulation of the vector "B" in a closed loop can be represented as the product of the magnetic constant m for the sum of currents:
Integral of B over dL = integral of Bl over dL = m Σ In
where n is the total number of conductors with multidirectional currents, covered by the imaginary circuit L of arbitrary shape.
Each current is counted in this formula as many times as it is completely covered by this circuit.
The final form of the obtained calculations for the total current law is greatly influenced by the environment in which the induced electromagnetic force (field) acts.
Influence of the environment
The considered ratios for the law of currents and fields acting not in a vacuum, but in a magnetic medium, acquire a slightly different form. In this case, in addition to the main current components, the concept of microscopic currents arising in a magnet, for example, or in any material similar to it, is introduced.
The required ratio is derived in full from the theorem on the vector circulation of magnetic induction B. In simple terms, it is expressed in the following form. The total value of the vector B when integrating along the selected contour is equal to the sum of the macrocurrents covered by it, multiplied by the coefficient of the magnetic constant.
As a result, the formula for "B" in the substance is determined by the expression:
Integral of B over dL = integral of Bl over dL = m(I+I1)
where: dL is a discrete element of the circuit directed along its bypass, Bl is a component in the direction of the tangent at an arbitrary point, bI and I1 are the conduction current and microscopic (molecular) current.
If the field acts in a medium consisting of arbitrary materials, microscopic currents characteristic of these structures must be taken into account.
These calculations are also true for a field created in a solenoid or in any other medium with finite magnetic permeability.
For reference
In the most complete and comprehensive CGS measurement system, the magnetic field strength is represented in oersteds (E). In another system in force (SI), it is expressed in amperes per meter (A / meter). Today, the oersted is gradually being replaced by a more convenient unit - ampere per meter. When translating the results of measurements or calculations from SI to CGS, the following ratio is used:
1 E = 1000 / (4π) A / m ≈ 79.5775 Ampere / meter.
In the final part of the review, we note that no matter what formulation of the law of total currents is used, its essence remains unchanged. In his own words, it can be represented as follows: it expresses the relationship between the currents that penetrate a given circuit and the magnetic fields created in the substance.
Finally, we recommend watching a useful video on the topic of the article:
Related materials:
- What is an electric field
- The dependence of the resistance of the conductor on temperature
- Nikola Tesla's greatest discoveries