החוק הנוכחי הכולל של שדה מגנטי: נוסחאות והגדרה

הנושא המוכר לרבים בשם "הנדסת חשמל" מכיל בתוכנו מספר חוקי יסוד הקובעים את עקרונות האינטראקציה הפיזית של שדה מגנטי. הם מרחיבים את פעולתם לאלמנטים שונים של מכשירים חשמליים, כמו גם למבנים ולסביבות המרכיבים שלהם. הפיזיקה של התהליכים המתרחשים בהם נוגעת למושגי יסוד כגון זרימות חשמל ושדות. חוק הזרם הכולל קובע את הקשר בין תנועת מטענים חשמליים לבין השדה המגנטי שנוצר על ידו (ליתר דיוק, עוצמתו). המדע המודרני טוען כי יישומו משתרע כמעט על כל הסביבות.

מהות החוק

החוק הנחשב, החל במעגלים מגנטיים, קובע את הקשר הכמותי הבא בין מרכיביו. זרימתו של וקטור השדה המגנטי בלולאה סגורה פרופורציונלית לסכום הזרמים הזורמים בו. כדי להבין את המשמעות הפיזית של חוק הזרם הכולל, יהיה עליך להכיר את הייצוג הגרפי של התהליכים המתוארים על ידו.

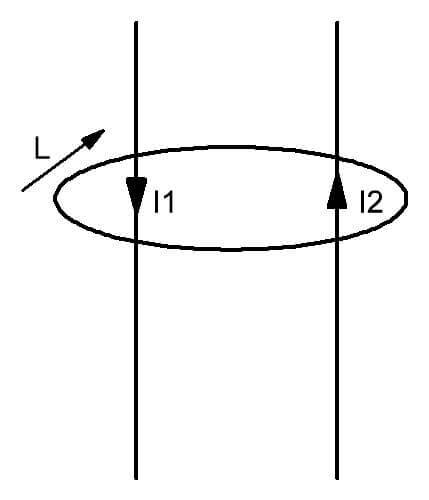
ניתן לראות מהאיור כי סביב שני מוליכים עם זרמים I1 ו- I2 הזורמים דרכם, נוצר שדה, מוגבל על ידי קו המתאר L. הוא מוצג כדמות סגורה בדמיון נפשי, שמישורו חדור מוליכים בעלי מטענים נעים. במילים פשוטות ניתן לבטא חוק זה כדלקמן. בנוכחות מספר זרמי חשמל דרך המשטח הדמיוני המכוסה בקווי המתאר L, נוצר בתוכו שדה מגנטי עם חלוקת עוצמות נתונה.

לכיוון התנועה החיובית של הווקטור, בהתאם לחוק המתאר של המעגל המגנטי, נבחרת התנועה עם כיוון השעון. זה גם דמוי.

הגדרה כזו של שדה הערבול שנוצר על ידי זרמים מניחה כי הכיוון של כל אחד מהזרמים יכול להיות שרירותי.

להשוואה! יש להבחין במבנה השדה המוצג והמנגנון המתאר אותו מהמחזור של הווקטור האלקטרוסטטי "E", שהוא תמיד אפס בעת עקיפת המתאר. כתוצאה מכך, שדה כזה מתייחס למבנים פוטנציאליים. מחזור הווקטור "B" של השדה המגנטי לעולם אינו אפס. לכן הוא נקרא "מערבולת".

מושגי יסוד

בהתאם לחוק הנדון, הגישה הפשוטה הבאה משמשת לחישוב שדות מגנטיים. הזרם הכולל מיוצג כסכום של מספר מרכיבים הזורמים דרך פני השטח המכוסים בלולאה סגורה L. ניתן להציג חישובים תיאורטיים כדלקמן:

1. סך השטף החשמלי החודר לקווי המתאר Σ I הוא הסכום הווקטורי של I1 ו- I2.
2. בדוגמה הנדונה, הנוסחה משמשת לקביעתה:
   ΣI = I1- I2 (מינוס לפני המונח השני פירושו כיווני הזרמים הפוכים).
3. הם, בתורם, נקבעים על פי החוק (הכלל) הידוע בהנדסת חשמל גימבל.

חוזק השדה המגנטי לאורך המתאר מחושב על בסיס החישובים המתקבלים בטכניקות מיוחדות. כדי למצוא אותו, יהיה עליך לשלב פרמטר זה על פני L באמצעות המשוואה של מקסוול, המוצגת באחת הצורות.ניתן ליישם אותו גם בצורה דיפרנציאלית, אך הדבר יסבך מעט את החישובים.

גישה אינטגרלית פשוטה יותר

אם נשתמש בייצוג הדיפרנציאלי, יהיה מאוד קשה לבטא את החוק הנוכחי הכולל בצורה פשוטה (במקרה זה, יש להכניס לתוכו רכיבים נוספים). אנו מוסיפים לכך ששדה המערבולת המגנטית הנוצרת על ידי זרמים הנעים בתוך המתאר, נקבע במקרה זה תוך התחשבות בזרם התזוזה, שתלוי בקצב השינוי בחשמל הַשׁרָאָה.

לכן, בפועל, הפופולרי ביותר ב- SOE הוא ייצוג נוסחאות לסך הזרמים בצורה של סיכום מקטעים קטנים מיקרוסקופיים של מעגל עם שדות מערבולת שנוצרים בהם. גישה זו כרוכה ביישום משוואת מקסוול בצורה אינטגרלית. כאשר הוא מיושם, קו המתאר מחולק למקטעים קטנים, שבקירוב הראשון נחשבים לקווי -ישר (על פי החוק, ההנחה היא כי השדה המגנטי אחיד). כמות זו, המסומנת כאום עבור קטע בודד אחד באורך ΔL של השדה המגנטי הפועל בחלל ריק, נקבעת כדלקמן:

אמ = HL * ΔL

המתח הכולל לאורך קו המתאר המלא L המוצג בקצרה בצורה אינטגרלית, מוצא על ידי הנוסחה הבאה:

UL = Σ HL * ΔL.

סך הכל החוק הנוכחי לוואקום

בצורתו הסופית, שנוסחה על פי כל כללי האינטגרציה, החוק הנוכחי הכולל נראה כך. ניתן לייצג את מחזור הווקטור "B" בלולאה סגורה כתוצר של הקבוע המגנטי M לסכום הזרמים:

אינטגרל של B מעל dL = אינטגרל של Bl מעל dL = M Σ ב

כאשר n הוא המספר הכולל של מוליכים עם זרמים רב כיוונים, המכוסים במעגל הדמיוני L בעל צורה שרירותית.

כל זרם נספר בנוסחה זו כמה פעמים שהוא מכוסה לחלוטין במעגל זה.

הצורה הסופית של החישובים המתקבלים לחוק הנוכחי הכולל מושפעת מאוד מהסביבה שבה פועל הכוח האלקטרומגנטי המושרה (שדה).

השפעת הסביבה

היחסים הנחשבים לחוק הזרמים והשדות הפועלים לא בחלל ריק, אלא במדיום מגנטי, רוכשים צורה מעט שונה. במקרה זה, בנוסף למרכיבי הזרם העיקריים, מוצג מושג הזרמים המיקרוסקופיים העולים במגנט, למשל, או בכל חומר דומה לו.

היחס הנדרש נגזר במלואו מהמשפט על מחזור הווקטורים של אינדוקציה מגנטית B. במילים פשוטות, זה בא לידי ביטוי בצורה הבאה. הערך הכולל של הווקטור B בעת השתלבות לאורך המתאר הנבחר שווה לסכום מקרו הזרמים המכוסים בו, מוכפל במקדם הקבוע המגנטי.

כתוצאה מכך, הנוסחה של "B" בחומר נקבעת על ידי הביטוי:

אינטגרל של B מעל dL = אינטגרל של Bl מעל dL = M(אני+אני1)

כאשר: dL הוא אלמנט נפרד של המעגל המכוון לאורך המעקף שלו, Bl הוא מרכיב בכיוון המשיק בנקודה שרירותית, bI ו- I1 הם זרם ההולכה והזרם המיקרוסקופי (מולקולרי).

אם השדה פועל במדיום המורכב מחומרים שרירותיים, יש לקחת בחשבון זרמים מיקרוסקופיים האופייניים למבנים אלה.

חישובים אלה נכונים גם לגבי השדה שנוצר בסולנואיד או בכל מדיום אחר בעל חדירות מגנטית סופית.

להשוואה

במערכת מדידת CGS השלמה והמקיפה ביותר, חוזק השדה המגנטי מיוצג ב- oersteds (E). במערכת אחרת בתוקף (SI) היא מתבטאת באמפר למטר (A / מטר). כיום, ה- oersted מתחלף בהדרגה ביחידה נוחה יותר - אמפר למטר. בעת תרגום תוצאות המדידות או החישובים מ- SI ל- CGS, נעשה שימוש ביחס הבא:

1 E = 1000 / (4π) A / m ≈ 79.5775 אמפר / מטר.

בחלק האחרון של הסקירה, נציין כי לא משנה באיזו נוסח של חוק הזרמים הכוללים משתמשים, מהותו נשארת ללא שינוי. במילותיו שלו, ניתן לייצגו באופן הבא: הוא מבטא את הקשר בין הזרמים המחלחלים למעגל נתון לבין השדות המגנטיים הנוצרים בחומר.

לבסוף, אנו ממליצים לצפות בסרטון שימושי בנושא המאמר:

חומרים קשורים:

• מהו שדה חשמלי
• תלות ההתנגדות של המנצח בטמפרטורה
• התגליות הגדולות ביותר של ניקולה טסלה