Hukum arus total untuk medan magnet: rumus dan definisi

Yang akrab bagi banyak mata pelajaran yang disebut "Teknik Elektro" berisi dalam programnya sejumlah hukum dasar yang menentukan prinsip-prinsip interaksi fisik untuk medan magnet. Mereka memperluas tindakan mereka ke berbagai elemen perangkat listrik, serta struktur dan lingkungan penyusunnya. Fisika dari proses yang terjadi di dalamnya menyangkut konsep dasar seperti aliran listrik dan medan. Hukum arus total menetapkan hubungan antara pergerakan muatan listrik dan medan magnet yang diciptakan olehnya (lebih tepatnya, intensitasnya). Ilmu pengetahuan modern mengklaim bahwa penerapannya meluas ke hampir semua lingkungan.

Inti dari hukum

Hukum yang dipertimbangkan, berlaku di sirkuit magnetik, menentukan hubungan kuantitatif berikut antara konstituennya. Sirkulasi vektor medan magnet dalam loop tertutup sebanding dengan jumlah arus yang mengalir melaluinya. Untuk memahami arti fisik dari hukum arus total, Anda perlu membiasakan diri dengan representasi grafis dari proses yang dijelaskan olehnya.

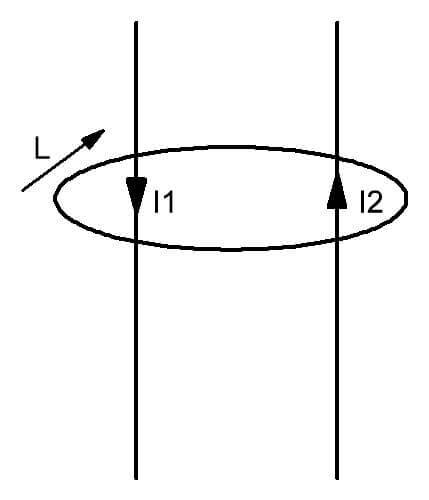
Dapat dilihat dari gambar bahwa di sekitar dua konduktor dengan arus I1 dan I2 yang mengalir melaluinya, terbentuk medan, dibatasi oleh kontur L. Itu diperkenalkan sebagai sosok tertutup yang dibayangkan secara mental, bidang yang ditembus oleh konduktor dengan muatan bergerak. Secara sederhana, hukum ini dapat dinyatakan sebagai berikut. Di hadapan beberapa aliran listrik melalui permukaan imajiner yang ditutupi oleh kontur L, medan magnet dengan distribusi intensitas tertentu terbentuk di dalamnya.

Untuk arah gerakan positif dari vektor, sesuai dengan hukum untuk kontur sirkuit magnetik, gerakan searah jarum jam dipilih. Itu juga divisualisasikan.

Definisi medan eddy seperti itu yang diciptakan oleh arus mengasumsikan bahwa arah masing-masing arus dapat berubah-ubah.

Sebagai referensi! Struktur medan yang diperkenalkan dan peralatan yang menjelaskannya harus dibedakan dari sirkulasi vektor elektrostatik "E", yang selalu nol ketika melewati kontur. Akibatnya, bidang seperti itu mengacu pada struktur potensial. Sirkulasi vektor "B" medan magnet tidak pernah nol. Itulah mengapa disebut "pusaran".

Konsep dasar

Sesuai dengan hukum yang dipertimbangkan, pendekatan sederhana berikut ini diterapkan untuk menghitung medan magnet. Arus total direpresentasikan sebagai jumlah dari beberapa komponen yang mengalir melalui permukaan yang ditutupi oleh loop tertutup L. Perhitungan teoritis dapat disajikan sebagai berikut:

1. Fluks listrik total yang menembus kontur I adalah jumlah vektor dari I1 dan I2.
2. Dalam contoh yang sedang dipertimbangkan, rumus digunakan untuk menentukannya:
   I = I1- I2 (minus sebelum suku kedua berarti arah arus berlawanan).
3. Mereka, pada gilirannya, ditentukan sesuai dengan hukum (aturan) yang terkenal dalam teknik listrik gimbal.

Kekuatan medan magnet di sepanjang kontur dihitung berdasarkan perhitungan yang diperoleh dengan menggunakan teknik khusus. Untuk menemukannya, Anda harus mengintegrasikan parameter ini di atas L menggunakan persamaan Maxwell, yang disajikan dalam salah satu bentuk.Ini juga dapat diterapkan dalam bentuk diferensial, tetapi ini akan sedikit memperumit perhitungan.

Pendekatan Integral Sederhana

Jika kita menggunakan representasi diferensial, akan sangat sulit untuk menyatakan hukum arus total dalam bentuk yang disederhanakan (dalam hal ini, komponen tambahan harus dimasukkan ke dalamnya). Kami menambahkan bahwa medan pusaran magnet, yang diciptakan oleh arus yang bergerak di dalam kontur, ditentukan dalam hal ini dengan mempertimbangkan arus perpindahan, yang tergantung pada laju perubahan listrik induksi.

Oleh karena itu, dalam praktiknya, yang paling populer di BUMN adalah representasi rumus untuk arus total dalam bentuk penjumlahan bagian-bagian kecil secara mikroskopis dari suatu rangkaian dengan medan pusaran yang dibuat di dalamnya. Pendekatan ini melibatkan penerapan persamaan Maxwell dalam bentuk integral. Ketika diterapkan, kontur dibagi menjadi segmen-segmen kecil, yang pada pendekatan pertama dianggap bujursangkar (menurut hukum, medan magnet diasumsikan seragam). Kuantitas ini, dilambangkan sebagai Um untuk satu bagian diskrit dengan panjang L medan magnet yang bekerja dalam ruang hampa, ditentukan sebagai berikut:

Um = HL * L

Tegangan total sepanjang kontur lengkap L, disajikan secara singkat dalam bentuk integral, ditemukan dengan rumus berikut:

UL = HL * L.

Hukum total saat ini untuk vakum

Dalam bentuk akhirnya, disusun menurut semua aturan integrasi, total hukum saat ini terlihat seperti ini. Sirkulasi vektor "B" dalam loop tertutup dapat direpresentasikan sebagai produk dari konstanta magnetik M untuk jumlah arus:

Integral B atas dL = integral Bl atas dL = M Dalam

di mana n adalah jumlah total konduktor dengan arus multiarah yang dicakup oleh kontur L bentuk sewenang-wenang yang dibayangkan.

Setiap arus dihitung dalam rumus ini sebanyak arus yang tercakup seluruhnya oleh rangkaian ini.

Bentuk akhir dari perhitungan yang diperoleh untuk hukum arus total sangat dipengaruhi oleh lingkungan di mana gaya elektromagnetik (medan) induksi bekerja.

Pengaruh lingkungan

Rasio yang dipertimbangkan untuk hukum arus dan medan, yang bertindak tidak dalam ruang hampa, tetapi dalam media magnetik, memperoleh bentuk yang sedikit berbeda. Dalam hal ini, selain komponen arus utama, konsep arus mikroskopis yang timbul dalam magnet, misalnya, atau dalam bahan apa pun yang serupa dengannya, diperkenalkan.

Rasio yang diperlukan diturunkan secara lengkap dari teorema pada sirkulasi vektor induksi magnetik B. Secara sederhana, itu dinyatakan dalam bentuk berikut. Nilai total vektor B ketika mengintegrasikan sepanjang kontur yang dipilih sama dengan jumlah arus makro yang dicakup olehnya, dikalikan dengan koefisien konstanta magnetik.

Akibatnya, rumus untuk "B" dalam zat ditentukan oleh ekspresi:

Integral B atas dL = integral Bl atas dL = M(Saya+Saya1)

di mana: dL adalah elemen diskrit dari rangkaian yang diarahkan sepanjang bypassnya, Bl adalah komponen dalam arah garis singgung pada titik sewenang-wenang, bI dan I1 adalah arus konduksi dan arus mikroskopis (molekul).

Jika medan bekerja dalam media yang terdiri dari bahan sembarang, karakteristik arus mikroskopis dari struktur ini harus diperhitungkan.

Perhitungan ini juga berlaku untuk medan yang dibuat dalam solenoida atau media lain dengan permeabilitas magnetik terbatas.

Sebagai referensi

Dalam sistem pengukuran CGS yang paling lengkap dan inklusif, kekuatan medan magnet direpresentasikan dalam oersteds (E). Dalam sistem lain yang berlaku (SI), dinyatakan dalam ampere per meter (A / meter). Hari ini, oersted secara bertahap digantikan oleh unit yang lebih nyaman - ampere per meter. Saat menerjemahkan hasil pengukuran atau perhitungan dari SI ke CGS, digunakan rasio sebagai berikut:

1 E = 1000 / (4π) A / m 79,5775 Ampere / meter.

Di bagian akhir tinjauan, kami mencatat bahwa apa pun rumusan hukum arus total yang digunakan, esensinya tetap tidak berubah. Dengan kata-katanya sendiri, itu dapat direpresentasikan sebagai berikut: itu mengungkapkan hubungan antara arus yang menembus sirkuit tertentu dan medan magnet yang dibuat dalam zat.

Akhirnya, kami sarankan menonton video yang bermanfaat tentang topik artikel:

Bahan terkait:

• Apa itu medan listrik
• Ketergantungan resistansi konduktor pada suhu
• Penemuan terbesar Nikola Tesla